Chris Gilliard and Hugh Culik — The New Pythagoreans

Chris Gilliard and Hugh Culik

A student’s initiation into mathematics routinely includes an encounter with the Pythagorean Theorem, a simple statement that describes the relationship between the hypotenuse and sides of a right triangle: the sum of the squares of the sides is equal to the square of the hypotenuse, i.e., A² + B² = C². The statement and its companion figure of a generic right triangle are offered as an interchangeable, seamless flow between geometric “things” and numbers (Kline 1980, 11). Among all the available theorems that might be offered as emblematic of mathematics, this one is held out as illustrative of a larger claim about mathematics and the Real. This use suggests that it is what W. J. T. Mitchell would call a “hypericon,” a visual paradigm that doesn’t “merely serve as [an] illustration to theory; [it] picture[s] theory” (1995, 49). Understood in this sense, the Pythagorean Theorem asserts a central belief of Western culture: that mathematics is the voice of an extra-human realm, a realm of fundamental, unchanging truth apart from human experience, culture, or biology. 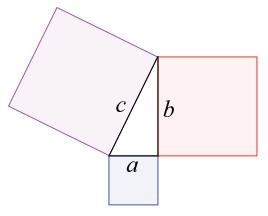It is understood as more essential than the world and as prior to it. Mathematics becomes an outlier among representational systems because numbers are claimed to be “ideal forms necessarily prior to the material ‘instances’ and ‘examples’ that are supposed to illustrate them and provide their content” (Rotman 2000, 147).[1] The dynamic flow between the figure of the right triangle and the formula transforms mathematical language into something akin to Christian concepts of a prelapsarian language, a “nomenclature of essences, in which word would have reflected thing with perfect accuracy” (Eagle 2007, 184). As the Pythagoreans styled it, the world is number (Guthrie 1962, 256). The image schools the child into the culture’s uncritical faith in the rhetoric of numbers, a sort of everyman’s version of the Pythagorean vision. Whatever the general belief in this notion, the nature of mathematical representations has been a central problematic of mathematics that appears throughout its history. The difference between the historical significance of this problematic and its current manifestation in the rhetoric of “Big Data” illustrates an important cultural anxiety.

Contemporary culture uses the Pythagorean Theorem’s image and formula as a hypericon that not only obscures problematic assumptions about the consistency and completeness of mathematics, but which also misrepresents the consistency and completeness of the material-world relationships that mathematics is used to describe.[2] This rhetoric of certainty, consistency, and completeness continues to infect contemporary political and ideological claims. For example, “Big Data” enthusiasts – venture capitalists, politicians, financiers, education reformers, policing strategists, et al. – often invoke a neo-Pythagorean worldview to validate their claims, claims that rest on the interplay of technology, analysis, and mythology (Boyd and Crawford 2012, 663). What is a highly productive problematic in the 2,500-year history of mathematics disappears into naïve assertions about the inherent “truth” of the algorithmic outputs of mathematically based technologies. When corporate behemoths like Pearson and Knewton (makers of an adaptive learning platform) participate in events such as the Department of Education’s 2012 “Datapalooza,” the claims become totalizing. Knewton’s CEO, Jose Ferreira, asserts, in a crescendo of claims, that “Knewton gets 5-10 million actionable data points per student per day”; and that tagging content “unlocks data.” In his terms, “work cascades out data” that is then subject to the various models the corporation uses to predict and prescribe the future. His claims of descriptive completeness are correct, he asserts, because “everything in education is correlated to everything else” (November 2012). The narrative of Ferreira’s claims is couched in fluid equivalences of data points, mathematical models, and a knowable future. Data become a metonym for not only the real student, but for the nature of learning and human cognition. In a sort of secularized predestination, the future’s origin in perfectly representational numbers produces perfect predictions of students’ performance. Whatever the scale of the investment dollars behind these New Pythagoreans, such claims lose their patina of objective certainty when placed in the history of the West’s struggle with mathematized claims about a putative “real.” For them, predictions are not the outcomes of processes; rather, predictions are revelations of a deterministic reality.[3]

A recent claim for a facial-recognition algorithm that identifies criminals normalizes its claims by simultaneously asserting and denying that “in all cultures and all periods of recorded human history, [is] the belief that the face alone suffices to reveal innate traits of a person” (Wu, Xiaolin, and Xi Zhang 2016, 1) The authors invoke the Greeks:

Aristotle in his famous work Prior Analytics asserted, ‘It is possible to infer character from features, if it is granted that the body and the soul are changed together by the natural affections’ (1)

The authors then remind readers that “the same question has captivated professionals (e.g., psychologists, sociologists, criminologists) and amateurs alike, across all cultures, and for as long as there are notions of law and crime. Intuitive speculations are abundant both in writing . . . and folklore.” Their work seeks to demonstrate that the question yields to a mathematical model, a model that is specifically a non-human intelligence: “In this section, we try to answer the question in the most mechanical and scientific way allowed by the available tools and data. The approach is to let a machine learning method explore the data and reveal the most discriminating facial features that tell apart criminals and non-criminals” (6). The rhetoric solves the problem by asserting an unchanging phenomenon – the criminal face – by invoking a mathematics that operates via machine learning. Problematic crimes such as “DWB” (driving while black) disappear along with history and social context.

Such claims rest on confused and contradictory notions. For the Pythagoreans, mathematics was not a representational system. It was the real, a reality prior to human experience. This claim underlies the authority of mathematics in the West. But simultaneously, it effectively operates as a response to the world, i.e., it is a re-presentation. As re-presentational, it becomes another language, and like other languages, it is founded on bias, exclusions, and incompleteness. These two notions of mathematics are resolved by seeing the representation as more “real” than the multiply determined events it re-presents. Nonetheless, once we say it re-presents the real, it becomes just another sign system that comes after the real. Often, bouncing back and forth between its extra-human status and its representational function obscures the places where representation fails or becomes an approximation. To data fetishists, “data” has a status analogous to that of “number” in the Pythagorean’s world. For them, reality is embedded in a quasi-mathematical system of counting, measuring, and tagging. But the ideological underpinnings, pedagogical assumptions, and political purposes of the tagging go unremarked; to do so would problematize the representational claims. Because the world is number, coders are removed from the burden of history and from the responsibility to examine the social context that both creates and uses their work.

The confluence of corporate and political forces validates itself through mathematical imagery, animated graphics, and the like. Terms such as “data-driven” and “evidence-based” grant the rhetoric of numbers a power that ignores its problematic assumptions. There is a pervasive refusal to recognize that data are artifacts of the descriptive categories imposed on the world. But “Big Data” goes further; the term is used in ways that perpetuate the antique notion of “number” by invoking numbers as distillations of certainty and a knowable universe. “Number” becomes decontextualized and stripped of its historical, social, and psychological origins. Because the claims of Big Data embed residual notions about the re-presentational power of numbers, and about mathematical completeness and consistency, they speak to such deeply embedded beliefs about mathematics, the most fundamental of which is the Pythagorean claim that the world is number. The point is not to argue whether mathematics is formal, referential, or psychological; rather, it is to place contemporary claims about “Big Data” in historical and cultural contexts where such issues are problematized. The claims of Big Data speak through a language whose power rests on longstanding notions of mathematics; however, these notions lose some of their power when placed in the context of mathematical invention (Rotman 2000, 4-7).

“Big Data” represents a point of convergence for residual mathematical beliefs, beliefs that obscure cultural frameworks and thus interfere with critique. For example, predictive policing tools are claimed to produce neutral, descriptive acts using machine intelligence. Berk asserts that “if you let the computer just snoop around in the dataset, it finds things that are unexpected by existing theory and works really substantially well to help forecast” (Berk 2011). In this view, Big Data – the numerical real – can be queried to produce knowledge that is not driven by any theoretical or ideological interest. Precisely because the world is presumed to be mathematical, the political, economic, and cultural frameworks of its operation can become the responsibility of the algorithm’s users. To this version of a mathematized real, there is no inherently ethical algorithmic action prior to the use of its output. Thus, the operation of the algorithm is doubly separated from its social contexts. First, the mathematics themselves are conceived as autonomous embodiments of a reality independent of the human; second, the effects of the algorithm – its predictions – are apart from values, beliefs, and needs that create the algorithm. The specific limits of historical and social context do not mathematically matter; the limits are determined by the values and beliefs of the algorithm’s users. The problematics of mathematizing the world are passed off to its customers. Boyd and Crawford identify three interacting phenomena that create the notion of Big Data: technology, analysis, and mythology (2012, 663). The mythological element embodies both dystopian and utopian narratives, and thus how we categorize reality. O’Neil notes that “these models are constructed not just from data but from the choices we make about which data to pay attention to – and which to leave out. Those choices are not just about logistics, profits, and efficiency. They are fundamentally moral” (2016, 218). On one hand, the predictive value depends on the moral, ethical, and political values of the user, a non-mathematical question. On the other hand, this division between the model and its application carves out a special arena where the New Pythagoreans claim that it operates without having to recognize social or historical contexts.

Whatever their commitment to number, the Pythagoreans were keenly aware that their system was vulnerable to discoveries that problematized their basic claim that the world is number. And they protected their beliefs through secrecy and occasionally through violence. Like the proprietary algorithms of contemporary corporations, their work was reserved for a circle of adepts/owners. First among their secrets was the keen understanding that an unnamable point on the number line would represent a rupture in the relationship of mathematics and world. If that relationship failed, with it would go their basis for belief in a knowable world. Their claims arose from within the concrete practices of Greek mathematics. For example, the Greeks portrayed numbers by a series of dots called Monads. The complex ratios used to describe geometric figures were understood to generate the world, and numbers were visualized in arrangements of stones (calculi). A 2 x 2 arrangement of stones had the form of a square, hence the term “square numbers.” Thus, it was a foundational claim that any point or quantity (because monads were conceived as material objects) have a corresponding number. Line segments, circumferences, and all the rest had to correspond to what we still call the “rational numbers”: 1, 2, 3 . . . and their ratios. Thus, the Pythagorean’s great claim – that the world is number – was vulnerable to the discovery of a point on the number line that could not be named as the ratio of integers.

Unfortunately for their claim, such numbers are common, and the great irony of the Pythagorean Theorem lies in the fact that it routinely generates numbers that are not ratios of integers. For example, a right triangle with sides one-unit long has a hypotenuse √2 units long (1² + 1² = C² i.e., 2 = C² i.e., √2 = C). Numbers such as √2 contradict the mathematical aspiration toward a completely representational system because they cannot be expressed as a ratio of integers, and hence their status as what are called “ir-rational” numbers.[4] A relatively simple proof demonstrates that they are neither odd nor even; these numbers exist in what is called a “surd” relationship to the integers, that is, they are silent – the meaning of “surd” – about each other. They literally cannot “speak” to each other. To the Pythagoreans, this appeared as a discontinuity in their naming system, a gap that might be the mark of a world beyond the generative power of number. Such numbers are, in fact, a new order of naming precipitated by the limited representational power of the prior naming system based on real numbers. But for the Pythagoreans, to look upon these numbers was to look upon the void, to discover that the world had no intrinsic order. Irrational numbers disrupted the Pythagorean project of mathematizing reality. This deeply religious impulse toward order underlies the aspiration that motivates the bizarre and desperate terminologies of contemporary data fetishists: “data-driven,” “evidence-based,” and even “Big Data,” which is usually capitalized to show the reification of number it desires.

Big Data appeals to a mathematical nostalgia for certainty that cannot be sustained in contemporary culture. O’Neil provides careful examples of how history, social context, and the data chosen for algorithmic manipulation do not – indeed cannot – matter in this neo-Pythagorean world. Like Latour, she historicizes the practices and objects that the culture pretends are natural. The ideological and political nature of the input becomes invisible, especially when algorithms are granted special proprietary status that converts them to what Pasquale calls a “black box” (2016). It is a problematic claim, but it can be made without consequence because it speaks in the language of an ancient mathematical philosophy still heard in our culture,[5] especially in education where the multifoliate realities of art, music, and critical writing are quashed by forces such as the Core Curriculum and its pervasive valorization of standardization. Such strategies operate in fear of the inconsistency and incompleteness of any representational relationship, a fear of epistemological silence that has lurked in the background of Western mathematics from its beginnings. To the Greeks, the irrationals represented a sort of mathematical aphasia. The irrational numbers such as √2 thus obtained emblematic values far beyond their mathematical ones. They inserted an irremediable gap between the world and the “word” of mathematics. Such knowledge was catastrophic – adepts were murdered for revealing the incommensurability of side and diagonal.[6] More importantly, the discovery deeply fractured mathematics itself. The gap in the naming system split mathematics into algebra (numerical) and geometry (spatial), a division that persisted for almost 2,000 years. Little wonder that the Greeks restricted geometry to measurements that were not numerical, but rather were produced through the use of a straightedge and compass. Physical measurement by line segments and circles rather than by a numerical length effectively sidestepped the threat posed by the irrational numbers. Kline notes, “The conversion of all of mathematics except the theory of whole numbers into geometry . . . forced a sharp separation between number and geometry . . . at least until 1600” (1980, 105). Once we recognize that the Pythagorean theorem is a hypericon, i.e., a visual paradigm that visualizes theory, we begin to see its extension into other fundamental mathematical “discoveries” such as Descartes’s creation of coordinate geometry. A deep anxiety about the gap between word and world is manifested in both mathematics as well as in contemporary claims about “Big Data.”

The division between numerical algebra and spatial geometry remained a durable feature of Western mathematics until problematized by social change. Geometry offered an elegant axiomatic system that satisfied the hierarchical impulse of the culture, and it worked in concert with the Aristotelian logic that dominated notions of truth. The Aristotelian nous and the Euclidian axioms seemed similar in ways that justified the hierarchical structure of the church and of traditional politics. They were part of a social fabric that bespoke an extra-human order that could be dis-covered. But with the rise of commercial culture came the need for careful records, computations, risk assessments, interest calculations, and other algebraic operations. The tension between algebra and geometry became more acute and visible. It was in this new cultural setting that Descartes’s work appeared. Descartes’s 1637 publication of La Géométrie confronted the terrors revealed in the irrationals embodied in the geometry/algebra divide by subordinating both algebra and geometry to a more abstract relationship. Turchin notes that Descartes re-unified geometry and arithmetic not by granting either priority or reducing either to the other; rather, in his language “the symbols do not designate number or quantities, but relations of quantities” (Turchin 1977, 196).

Rotman directly links concepts of number to this shifting relationship of algebra and geometry and even to the status of numbers such as zero:

During the fourteenth century, with the emergence of mercantile / capitalism in Northern Italy, the handling of numbers passed . . . to merchants, artisan-scientists, architects . . . for whom arithmetic was an essential prerequisite for trade and technology . . . . The central role occupied by double-entry book-keeping (principle of the zero balance) and the calculational demands of capitalism broke down any remaining resistance to the ‘infidel symbol’ of zero. (1987, 7-8)

The emergence of the zero is an index to these changes, not the revelation of a pre-existing, extra-human reality. Similarly, Alexander’s history of the calculus places its development in the context of Protestant notions of authority (2014, 140-57). He emphasizes that the methodologies of the sciences and mathematics began to serve as political models for scientific societies: “if reasonable men of different backgrounds and convictions could meet to discuss the workings of nature, why could they not do the same in matters that concerned the state?” (2014, 249). Again, in the case of the calculus, mathematics responds to the emerging forces of the Renaissance: individualism, capitalism, and Protestantism. Certainly, the ongoing struggle with irrational numbers extends from the Greeks to the Renaissance, but the contexts are different. For the Greeks, the generative nature of number was central. For 17^th Century Europe, the material demands of commercial life converged with religious, economic, and political shifts to make number a re-presentational tool.

The turmoil of that historical moment suggests the turmoil of our own era in the face of global warfare, climate change, over-population, and the litany of other catastrophes we perpetually await.[7] In both cases, the anxiety produces impulses to mathematize the world and thereby reveal a knowable “real.” The current corporate fantasy that the world is a simulation is the fantasy of non-mathematicians (Elon Musk and Sam Altman) to embed themselves in a techno-centric narrative of the power of their own tools to create themselves. While this inexpensive version of Baudrillard’s work might seem sophomoric, it nevertheless exposes the impulse to contain the visceral fear that a socially constructed world is no different from solipsism’s chaos. It seems a version of the freshman student’s claim that “Everything’s just opinion” or the plot of another Matrix film. They speak/act/claim that their construction of meaning is equal to any other — the old claim that Hitler and Mother Teresa are but two equally valid “opinions”. They don’t know that the term/concept is social construction, and their radical notions of the individual prevent them from recognizing the vast scope, depth, and stabilizing power of social structures. They are only the most recent example of how social change exacerbates the misuse of mathematics.

Amid these sorts of epistemic shifts, Renaissance mathematics underwent its own transformations. Within a fifty-year span (1596-1646), Descartes, Newton, and Leibniz are born. Their major works appear, respectively, in 1637, 1666, and 1675, a burst of innovation that cannot be separated from the shifts in education, economics, religion, and politics that were then sweeping Europe. Porter notes that statistics emerges alongside the rising modern state of this era. Managing the state’s wealth required profiles of populations. Such mathematical profiling began in the mid-1600s, with the intent to describe the state’s wealth and human resources for the creation of “sound, well-informed state policy” (Porter 1986, 18). The notion of probabilities, samples, and models avoids the aspirations that shaped earlier mathematics by making mathematics purely descriptive. Hacking suggests that the delayed appearance of probability arises from five issues: 1) an obsession with determinism and personal fatalism; 2) the belief that God spoke through randomization and thus, a theory of the random was impious; 3) the lack of equiprobable events provided by standardized objects, e.g., dice; 4) the lack of economic drivers such as insurances and annuities; and 5) the lack of a workable calculus needed for the computation of probability distributions (Davis and Hersh 1981, 21). Hacking finds these insufficient and suggests that as authority was relocated in nature and not in the words of authorities, this led to the observation of frequencies.[8] Alongside the fierce opposition of the Church to the zero, understood as the absence of God, and to the calculus, understood as an abandonment of material number, the shifting mathematical landscape signals the changes that began to affect the longstanding status of number as a sort of prelapsarian language.

Mathematics was losing its claims to completeness and consistency, and the incommensurables problematized that. Newton and Leibniz “de-problematized” irrationals, and opened mathematics to a new notion of approximation. The central claims about mathematics were not disproved; worse, they were set aside as unproductive conflations of differences between the continuous and the discrete. But because the church saw mathematics as “true” in a fashion inextricable from other notions of the truth, it held a special status. Calculus became a dangerous interest likely to call the Inquisition to action. Alexander locates the central issue as the irremediable conflict between the continuous and the discrete, something that had been the core of Zeno’s paradoxes (2014). The line of mathematical anxieties stretches from the Greeks into the 17^th Century. These foundational understandings seem remote and abstract until we see how they re-appear in the current claims about the importance of “Big Data.” The term legitimates its claims by resonating with other responses to the anxiety of representation.

The nature of the hypericon perpetuates the notion of a stable, knowable reality that rests upon a non-human order. In this view, mathematics is independent of the world. It existed prior to the world and does not depend on the world; it is not an emergent narrative. The mathematician discovers what is already there. While this viewpoint sees mathematics as useful, mathematics is prior to any of its applications and independent of them. The parallel to religious belief becomes obvious if we substitute the term “God” for “mathematics”; the notions of a self-existing, self-knowing, and self-justifying system are equally applicable (Davis and Hersh 1981, 232-3). Mathematics and religion share in a fundamental Western belief in the Ideal. Taken together, they reveal a tension between the material and the eternal that can be mediated by specific languages. There is no doubt that a simplified mathematics serves us when we are faced with practical problems such as staking out a rectangular foundation for a house, but beyond such short-term uses lie more consequential issues, e.g., the relation of the continuous and the discrete, and between notions of the Ideal and the socially constructed. These larger paradoxes remain hidden when assertions of completeness, consistency, and certainty go unchallenged. In one sense, the data fetishists are simply the latest incarnation of a persistent problem: understanding mathematics as culturally situated.

Again, historicizing this problem addresses the widespread willingness to accept their totalistic claims. And historicizing these claims requires a turn to established critical techniques. For example, Rotman’s history of the zero turns to Derrida’s Of Grammatology to understand the forces that complicated and paralyzed the acceptance of zero into Western mathematics (1987). He turns to semiotics and to the work of Ricoeur to frame his reading of the emergence of the zero in the West during the Renaissance. Rotman, Alexander, desRaines, and a host of mathematical historians recognize that the nature of mathematical authority has evolved. The evolution lurks in the role of the irrational numbers, in the partial claims of statistics, and in the approximations of the calculus. The various responses are important as evidence of an anxiety about the limits of representation. The desire to resolve such arguments seems revelatory. All share an interest in the gap between the aspirations of systematic language and its object: the unnamable. That gap is iconic, an emblem of its limits and the functions it plays in the generation of novel responses to the threat of an inarticulable void; its history exposes the powerful attraction of the claims made for Big Data.

By the late 1800s, questions of systematic completeness and consistency grew urgent. For example, they appeared in the competing positions of Frege and Hilbert^, and they resonated in the direction David Hilbert gave to 20^th Century mathematics with his famed 23 questions (Blanchette 2014). The second of these specifically addressed the problem of proving that mathematical systems could be both complete and consistent. This question deeply influenced figures such as Bertrand Russell, Ludwig Wittgenstein, and others.^[9] Hilbert’s question was answered in 1931 by Gödel’s theorems that demonstrated the inherent incompleteness and inconsistency of arithmetic systems. Gödel’s first theorem demonstrated that axiomatic systems would necessarily have true statements that could be neither proven nor disproven; his second theorem demonstrated that such systems would necessarily be inconsistent. While mathematicians often take care to note that his work addresses a purely mathematical problem, it nevertheless is read metaphorically. As a metaphor, it connects the problematic relationship of natural and mathematical languages. This seems inevitable because it led to the collapse of the mathematical aspiration for a wholly formal language that does not require what is termed ‘natural’ language, that is, for a system that did not have to reach outside of itself. Just as John Craig’s work exemplifies the epistemological anxieties of the late eighteenth century,[10] so also does Gödel’s work identify a sustained attempt of his own era to demonstrate that systematic languages might be without gaps.

Gödel’s theorems rely on a system that creates specialized numbers for symbols and the operations that relate them. This second-order numbering enabled him to move back and forth between the logic of statements and the codes by which they were represented. His theorems respond to an enduring general hope for complete and consistent mappings of the world with words, and each embeds a representational failure.  Craig was interested in the loss of belief in the gospels; Pythagoras feared the gaps in the number line represented by the irrational numbers, and Gödel identified the incompleteness and inconsistency of axiomatic systems. To the dominant mathematics of the early 20^th Century, the value of the question to which Gödel addresses himself lies in the belief that an internally complete mathematical map would be the mark of either of two positions: 1) the purely syntactic orderliness of mathematics, one that need not refer to any experiential world (this is the position of Frege, Russell, and Hilbert); or 2) the emergence of mathematics alongside concrete, human experience. Goldstein argues that these two dominant alternatives of the late eighteenth and early twentieth centuries did not consider the aprioricity of mathematics to constitute an important question, but Gödel offered his theorems as proofs that served exactly that idea. His demonstration of incompleteness does not signal a disorderly cosmos; rather, it argues that there are arithmetic truths that lie outside of formalized systems; as Goldstein notes, “the criteria for semantic truth could be separated from the criteria for provability” (2006, 51). This was an argument for mathematical Platonism. Goldstein’s careful discussion of the cultural framework and the meta-mathematical significance of Gödel’s work emphasizes that it did not argue for the absence of any extrinsic order to the world (51). Rather, Gödel was consciously demonstrating the defects in a mathematical project begun by Frege, addressed in the work of Russell and Whitehead, and enshrined by Hilbert as essential for converting mathematics into a profoundly isolated system whose orderliness lay in its internal consistency and completeness.[11] Similarly, his work also directly addressed questions about the a priori nature of mathematics challenged by the Vienna Circle. Paradoxically, by demonstrating that a foundational system – arithmetic – was not consistent and complete, the argument that mathematics was simply a closed, self-referential system could be challenged and opened to meta-mathematical claims about epistemological problems.

Gödel’s work, among other things, argues for essential differences between human thought and mathematics. Gödel’s work has become imbricated in a variety of discourses about representation, the nature of the mind, and the nature of language. Goldstein notes:

The structure of Gödel’s proof, the use it makes of ancient paradox [the liar’s paradox], speaks at some level, if only metaphorically, to the paradoxes in the tale that the twentieth century told itself about some of its greatest intellectual achievements – including, of course, Gödel’s incompleteness theorems. Perhaps someday a historian of ideas will explain the subjectivist turn taken by so many of the last century’s most influential thinkers, including not only philosophers but hard-core scientists, such as Heisenberg and Bohr. (2006, 51)

At the least, his work participated in a major consideration of three alternative understandings of symbolic systems: as isolated, internally ordered syntactic systems, as accompaniments of experience in the material world, or as the a priori realities of the Ideal. Whatever the immensely complex issues of these various positions, Gödel is the key meta-mathematician/logician whose work describes the limits of mathematical representation through an elegant demonstration that arithmetic systems – axiomatic systems – were inevitably inconsistent and incomplete. Depending on one’s aspirations for language, this is either a great catastrophe or an opening to an infinite world of possibility where the goal is to deploy a paradoxical stance that combines the assertion of meaning with its cancellation. This double position addresses the problem of representational completeness.

This anxiety became acute during the first half of the twentieth century as various discourses deployed strategies that exploited this heightened awareness of the intrinsic incompleteness and inconsistency of systematic knowledge. Whatever their disciplinary differences – neurology, psychology, mathematics – they nonetheless shared the sense that recognizing these limits was an opportunity to understand discourse both from within narrow disciplinary practices and from without in a larger logical and philosophical framework that made the aspiration toward completeness quaint, naïve, and unproductive. They situated the mind as a sort of boundary phenomenon between the deployment of discourses and an extra-linguistic reality. In contrast to the totalistic claims of corporate spokesmen and various predictive software, this sensibility was a recognition that language might always fail to re-present its objects, but that those objects were nonetheless real and expressible as a function of the naming process viewed from yet another position. An important corollary was that these gaps were not only a token for the interplay of word and world, but were also an opportunity to illuminate the gap itself. In short, symbol systems seemed to stand as a different order of phenomena than whatever they proposed to represent, and the result was a burst of innovative work across a variety of disciplines.

Data enthusiasts sometimes participate in a discredited mathematics, but they do so in powerfully nostalgic ways that resonate with the amorphous Idealism infused in our hierarchical churches, political structures, aesthetics, and epistemologies. Thus, Big Data enthusiasts speak through the residue of a powerful historical framework to assert their own credibility. For these New Pythagoreans, mathematics remains a quasi-religious undertaking whose complexity, consistency, sign systems, and completeness assert a stable, non-human order that keeps chaos at bay. However, they are stepping into an issue more fraught than simply the misuses and misunderstanding of the Pythagorean Theorem. The historicized view of mathematics and their popular invocation of mathematics diverge at the point that anxieties about the representational failure of languages become visible. We not only need to historicize our understanding of mathematics, but also to identify how popular and commercial versions of mathematics are nostalgic fetishes for certainty, completeness, and consistency. Thus, the authority of algorithms has less to do with their predictive power than their connection to a tradition rooted in the religious frameworks of Pythagoreanism. Critical methods familiar to the humanities – semiotics, deconstruction, psychology – build a sort of critical braid that not only re-frames mathematical inquiry, but places larger question about the limits of human knowledge directly before us; this braid forces an epistemological modesty that is eventually ethical and anti-authoritarian in ways that the New Pythagoreans rarely are.

Immodest claims are the hallmark of digital fetishism, and are often unabashedly conscious. Chris Anderson, while Editor-in-Chief of Wired magazine, infamously argued that “the data deluge makes the scientific method obsolete” (2008). He claimed that distributed computing, cloud storage, and huge sets of data made traditional science outmoded. He asserted that science would become mathematics, a mathematical sorting of data to discover new relationships:

At the petabyte scale, information is not a matter of simple three and four-dimensional taxonomy and order but of dimensionally agnostic statistics. It calls for an entirely different approach, one that requires us to lose the tether of data as something that can be visualized in its totality. It forces us to view data mathematically first and establish a context for it later.

“Agnostic statistics” would be the mechanism that for precipitating new findings. He suggests that mathematics is somehow detached from its contexts and represents the real through its uncontaminated formal structures. In Anderson’s essay, the world is number. This neo-Pythagorean claim quickly gained attention, and then wilted in the face of scholarly response such as that of Pigliucci (2009, 534).

Anderson’s claim was both a symptom and a reinforcement of traditional notions of mathematics that extend far back into Western history. Its explicit notions of mathematics stirred two kinds of anxiety: one reflected a fear of a collapsed social project (science) and the other reflected a desperate hunger for a language – mathematics – that penetrated the veil drawn across reality and made the world knowable. Whatever the collapse of his claim, similar ones such as those of the facial phrenologists continue to appear. Without history – mathematical, political, ideological – “data” acquires a material status much as number did for the Greeks, and this status enables statements of equality between the messiness of reality and the neatness of formal systems. Part of this confusion is a common misunderstanding of the equals sign in popular culture. The “sign” is a relational function, much as the semiotician’s signified and signifier combine to form a “sign.” However, when we mistreat treat the “equals sign” as a directional, productive operation, the nature of mathematics loses its availability to critique. It becomes a process outside of time that generates answers by re-presenting the real in a language. Where once a skeptical Pythagorean might be drowned for revealing the incommensurability of side and diagonal, proprietary secrecy now threatens a sort of legalized financial death for those who violate copyright (Pasquale 2016, 142). Pasquale identifies the “creation of invisible powers” as a hallmark of contemporary, algorithmic culture (2016, 193). His invaluable work recovers the fact that algorithms operate in a network of economic, political, and ideological frameworks, and he carefully argues the role of legal processes in resisting the control that algorithms can impose on citizens.

Pasquale’s language is not mathematical, but it shares with scholars like Rotman and Goldstein an emphasis on historical and cultural context. The algorithm is made accountable if we think of it as an act whose performance instantiates digital identities through powerful economic, political, and ideological narratives. The digitized individual does not exist until it becomes the subject of such a performance, a performance which is framed much as any other performance is framed: by the social context, by repetition, and through embodiment. Digital individuals come into being when the algorithmic act is performed, but they are digital performances because of the irremediable gap between any object and its re-presentation. In short, they are socially constructed. This would be of little import except that these digital identities begin as proxies for real bodies, but the diagnoses and treatments are imposed on real, social, psychological, flesh beings. The difference between digital identity and human identity can be ignored if the mathematized self is isomorphic with the human self. Thus, algorithmic acts entangle the input > algorithm > output sequence by concealing layers of problematic differences: digital self and human self; mathematics and the Real; test inputs and test outputs, scaling, and input and output. The sequence loses its tidy sequential structure when we recognize that the outputs are themselves data and often re-enter the algorithm’s computations by their transfer to third parties whose information returns for re-processing. A somewhat better version of the flow would be data1 > algorithm > output > data2 > algorithm > output > data3. . . . with the understanding that any datum might re-enter the process. The sequence suggests how an object is both the subject of its context and a contributor to that context. The threat of a constricting output looms precisely because there is a decreasing room for what de Certeau calls “le perruque” (1988, 25), i.e, the inefficiencies where unplanned innovation appears. And like any text, it requires a variety of analytic strategies.

We have learned to think of algorithms in directional terms. We understand them as transformative processes that operate upon data sets to create outputs. The problematic relationships of data > algorithm > output become even more visible when we recognize that data sets have already been collected according to categories and processes that embody political, economic, and ideological biases. The ideological origin of the collected data – the biases of the questions posed in order to generate “inputs” – are yet another kind of black box, a box prior to the black box of the algorithm, a prior structure inseparable from the algorithm’s hunger for (using the mathematicians’ language) a domain upon which it can act to produce a range of results. The nature of the algorithm controls what items from the domain (data set) can be used, and on the other hand, the nature of the data set controls what the algorithm has available to act upon and transform into descriptive and prescriptive claims. The inputs are as much a black box as the algorithm itself. Thus, opaque algorithms operate upon opaque data sets (Pasquale 2016, 204) in ways that nonetheless embody the inescapable “politics of large numbers” that is the topic of Desrosières and Naish’s history of statistical reasoning (2002). This interplay forces us to recognize that the algorithm inherits biases, and that then they are compounded by operations within these two algorithmic boxes to become doubly biased outputs. It might be more revelatory to term the algorithmic process as “stimuli” > algorithm > “responses.” Re-naming “input” as “stimuli” emphasizes the selection process that precedes the algorithmic act; re-naming “output” as “response” establishes the entire process as human, cultural, and situated. This is familiar territory to psychology. Digital technologies are texts whose complexity emerges when approached using established tools for textual analysis. Rotman and other mathematicians directly state their use of semiotics. They turn to phenomenology to explicate the reader/writer interaction, and they approach mathematical texts with terms like narrator, self-referential and recursion. Most of all, they explore the problem of mathematical representation when mathematics itself is complicated by its referential, formal, and psychological statuses.

The fetishization of mathematics is a fundamental strategy for exempting digital technologies from theory, history, and critique. Two responses are essential: first, to clarify the nostalgic mathematics at work in the mathematical rhetoric of Big Data and its tools; and second, to offer analogies that step beyond naïve notions of re-presentation to more productive critiques. Analogy is essential because analogy is itself a performance of the anti-representational claim that digital technologies need to be understood as socially constructed by the same forces that instantiate any technology. Bruno Latour frames the problem of the critical stance as three-dimensional:

The critics have developed three distinct approaches to talking about our world: naturalization, socialization and deconstruction . . . . When the first speaks of naturalized phenomena, then societies, subjects, and all forms of discourse vanish. When the second speaks of fields of power, then science, technology, texts, and the contents of activities disappear. When the third speaks of truth effects, then to believe in the real existence of brain neurons or power plays would betray enormous naiveté. Each of these forms of criticism is powerful in itself but impossible to combine with the other. . . . Our intellectual life remains recognizable as long as epistemologists, sociologists, and deconstructionists remain at arm’s length, the critique of each group feeding on the weaknesses of the other two. (1993, 5-6)

Latour then asks, “Is it our fault if the networks are simultaneously real, like nature, narrated, like discourse, and collective like society?” (6). He goes on to assert, “Analytic continuity has become impossible” (7). Similarly, Rotman’s history of the zero finds that the concept problematizes the hope that a “field of entities” exists prior to “the meta-sign which both initiates the signifying system and participates within it as a constituent sign”; he continues, “the simple picture of an independent reality of objects providing a pre-existing field of referents for signs conceived after them . . . cannot be sustained” (1987, 27). Our own approach is heterogeneous; we use notions of fetish, re-presentation, and Gödelian metaphor to try and bypass the critical immunity conferred on digital technologies by the naturalistic mathematical claims that immunize it against critique.

Whether we use Latour’s description of the mutually exclusive methods of talking about the world – naturalization, socialization, deconstruction – or if we use Rotman’s three starting points for the semiotic analysis of mathematical signs – referential, formal, and psychological – we can contextualize the claims of the Big Data fetishists so that the manifestations of Big Data thinking – policing practices, financial privilege, educational opportunity – are not misrepresented as only a mathematical/statistical question about assessing the results of supposedly neutral interventions, decisions, or judgments. If we are confined to those questions, we will only operate within the referential domains described by Rotman or the realm of naturalization described by Latour. The claims of an a-contextual validity violate the consequence of their contextual status by claiming that operations, uses, and conclusions are exempt from the aggregated array of partial theorizations, applied, in this case, to mathematics. This historical/critical application reveals the contradictory world concealed and perpetuated by the corporatized mathematics of contemporary digital culture. However, deploying a constellation of critical methods – historical, semiotic, psychological – prevents the critique from falling prey to the totalism that afflicts the thinking of these New Pythagoreans. This array includes concepts such as fetishization from the pre-digital world of psychoanalysis.

The concept of the fetish has fallen on hard times as the star of psychoanalysis sinks into the West’s neurochemical sea. But its original formulation remains useful because it seeks to address the gap between representational formulas and their objects. For example – drawing on the quintessential heterosexual, male figure who is central to psychoanalysis – the male shoe fetishist makes no distinction between a pair of Louboutins and the “normal” object of his sexual desire. Fenichel asserts (1945, 343) that such fetishization is “an attempt to deny a truth known simultaneously by another part of the personality,” and enables the use of denial. Such explanations may seem quaint, but that is not the point. The point is that within one of the most powerful metanarratives of the past century – psychoanalysis – scientists faced the contorted and defective nature of human symbolic behavior in its approach to a putative “real.” The fetish offers an illusory real that protects the fetishist against the complexities of the real. Similarly, the New Pythagoreans of Big Data offer an illusory real – a misconstrued mathematics – that often paralyzes resistance to their profit-driven, totalistic claims. In both cases, the fetish becomes the “real” while simultaneously protecting the fetishist from contact with whatever might be more human and more complex.

Wired Magazine’s “daily fetish” seems an ironic reversal of the term’s functional meaning. Its steady stream of technological gadgets has an absent referent, a hyperreal as Baudrillard styles it, that is exactly the opposite of the material “real” that psychoanalysis sees as the motivation of the fetish. In lived life, the anxiety is provoked by the real; in digital fetishism, the anxiety is provoked by the absence of the real. The anxiety of absence provokes the frenzied production of digital fetishes. Their inevitable failure – because representation always fails – drives the proliferation of new, replacement fetishes, and these become a networked constellation that forms a sort of simulacrum: a model of an absence that the model paradoxically attempts to fill. Each failure accentuates the gap, thereby accentuating the drive toward yet another digital embodiment of the missing part. Industry newsletters exemplify the frantic repetition required by this worldview. For example, Edsurge proudly reports an endless stream of digital edtech products, each substituting for the awkward, fleshly messiness of learning. And each substitution claims to validate itself via mathematical claims of representation. And almost all fade away as the next technology takes its place. Endless succession.

This profusion of products clamoring to be the “real” object suggests a sort of cultural castration anxiety, a term that might prove less outmoded if we note the preponderance of males in the field who busily give birth to objects with the characteristics of the living beings they seek to replace.[12] The absence at the core of this process is the unbridgeable gap between word and world. Mathematics is especially useful to such strategies because it is embedded in the culture as both the discoverer and validator of objective true/false judgments. These statements are understood to demonstrate a reality that “exists prior to the mathematical act of investigating it” (Rotman 2000, 6). It provides the certainty, the “real” that the digital fetish simultaneously craves and fears. Mathematics short-circuits the problematic question that drives the anxiety about a knowable “real.” The point here is not to revive psychoanalytic thinking, but rather to see how an anxiety mutates and invites the application of critical traditions that themselves embody a response to the incompleteness and inconsistency of sign systems. The psychological model expands into the destabilized social world of digital culture.

The notion of mathematics as a complete and consistent equivalent of the real is a longstanding feature of Western thought. It both creates and is created by the human need for a knowable real. Mathematics reassures the culture because its formal characteristics seem to operate without referents in the real world, and thus its language seems to become more real than any iteration of its formal processes. However, within mathematical history, the story is more convoluted, in part because of the immense practical value of applied mathematics. While semiotic approaches to the history engage and describe the social construction of mathematics, an important question remains about the completeness and consistency of mathematical systems. The history of this concern connects both the technical question and the popular interest in the power of languages – natural and/or mathematical – to represent the real. Again, these are not just technical, expert questions; they leak into popular metaphor because they embody a larger cultural anxiety about a knowable real. If Pythagorean notions have affected the culture for 2500 years, we want to claim that contemporary culture embodies the anxiety of uncertainty that is revealed not only in its mathematics, but also in the contemporary arguments about algorithmic bias, completeness, and consistency.

The nostalgia for a fully re-presentational sign system becomes paired with the digital technologies – software, hardware, networks, query strategies, algorithms, black boxes – that characterize daily life. However, this nostalgic rhetoric has a naïveté that embodies the craving for a stable and knowable external world. The culture often responds to it through objects inscribed with the certainty imputed to mathematics, and thus these digital technologies are felt to satisfy a deeply felt need. The problematic nature of mathematics matters little in terms of personalized shopping choices or customizing the ideal playlist. Although these systems rarely achieve the goal of “knowing what you want before you want it,” we rarely balk at the claim because the stakes are so low. However, where these claims have life-altering, and in some cases life and death implications – education, policing, health care, credit, safety net benefits, parole, drone targets – we need to understand them so they can be challenged, and where needed, resisted. Resistance addresses two issues:

1. That the traditional mystery and power of number seem to justify the refusal of transparency. The mystified tools point upward to the supposed mysterium of the mathematical realm.
2. That the genuflection before the mathematical mysterium has an insatiable hunger for illustrations that show the world is orderly and knowable.

Together, these two positions combine to assert the mythological status of mathematics, and set it in opposition to critique. However, it is vulnerable on several fronts. As Pasquale makes clear, legislation – language in action – can begin the demystification; proprietary claims are mundane imitations of the old Pythagorean illusions; outside of political pressure and legislation, there is little incentive for companies to open their algorithms to auditing. However, once pried open by legislation, the wizard behind the curtain and the Automated Turk show their hand. With transparency comes another opportunity: demythologizing technologies that fetishize the re-presentational nature of mathematics.

_____

Chris Gilliard’s scholarship concentrates on privacy, institutional tech policy, digital redlining, and the re-inventions of discriminatory practices through data mining and algorithmic decision-making, especially as these apply to college students.

Hugh Culik teaches at Macomb Community College. His work examines the convergence of systematic languages (mathematics and neurology) in Samuel Beckett’s fiction.

Back to the essay

_____

Notes

[1] Rotman’s work along with Amir Alexander’s cultural history of the calculus (2014) and Rebecca Goldstein’s (2006) placement of Gödel’s theorems in the historical context of mathematics’ conceptual struggle with the consistency and completeness of systems exemplify the movement to historicize mathematics. Alexander and Rotman are mathematicians, and Goldstein is a logician.

[2] Other mathematical concepts have hypericonic status. For example, triangulation serves psychology as a metaphor for a family structure that pits two members against a third. Politicians “triangulate” their “position” relative to competing viewpoints. But because triangulation works in only two dimensions, it produces gross oversimplifications in other contexts. Nora Culik (pers. comm.) notes that a better metaphor would be multilateration, a measurement of the time difference between the arrival of a signal with at least two known points and another one that is unknown, to generate possible locations; these take the shape of a hyperboloid, a metaphor that allows for uncertainty in understanding multiply determined concepts. Both re-present an object’s position, but each carries implicit ideas of space.

[3] Faith in the representational power of mathematics is central to hedge funds. Bridgewater Associates, a fund that manages more than $150 billion US, is at work building a piece of software to automate the staffing for strategic planning. The software seeks to model the cognitive structure of founder Raymond Dalio, and is meant to perpetuate his mind beyond his death. Dalio variously refers to the project as “The Book of the Future,” “The One Thing,” and “The Principles Operating System.” The project has drawn the enthusiastic attention of many popular publications such as The Wall Street Journal, Forbes, Wired, Bloomberg, and Fortune. The project’s model seems to operate on two levels: first, as a representation of Dalio’s mind, and second a representation of the dynamics of investing.

[4] Numbers are divided into categories that grow in complexity. The development of numbers is an index to the development of the field (Kline, Mathematical Thought, 1972). For a careful study of the problematic status of zero, see Brian Rotman, Signifying Nothing: The Semiotics of Zero (1987). Amir Aczel, Finding Zero: A Mathematician’s Odyssey to Uncover the Origins of Numbers (2015) offers a narrative of the historical origins of number.

[5] Eugene Wigner (1959) asserts an ambiguous claim for a mathematizable universe. Responses include Max Tegmark’s “The Mathematical Universe” (2008) which sees the question as imbricated in a variety of computational, mathematical, and physical systems.

[6] The anxiety of representation characterizes the shift from the literary moderns to the postmodern. For example, Samuel Beckett’s intense interest in mathematics and his strategies – literalization and cancellation – typify the literary responses to this anxiety. In his first published novel, Murphy (1938), one character mentions “Hypasos the Akousmatic, drowned in a mud puddle . . . for having divulged the incommensurability of side and diagonal” (46). Beckett uses detailed references to Descartes, Geulcinx, Gödel, and 17^th Century mathematicians such as John Craig to literalize the representational limits of formal systems of knowledge. Andrew Gibson’s Beckett and Badiou provides a nuanced assessment of the mathematics, literature, and culture (2006) in Beckett’s work.

[7] See Frank Kermode, The Sense of an Ending: Studies in the Theory of Fiction with a New Epilogue (2000) for an overview of the apocalyptic tradition in Western culture and the totalistic responses it evokes in politics. While mathematics dealt with indeterminacy, incompleteness, inconsistency and failure, the political world simultaneously saw a countervailing regressive collapse: Mein Kampf in 1925, the Soviet Gulag in 1934; Hitler’s election as Chancellor of Germany in 1933; the fascist bent of Ezra Pound, T. S. Eliot’s After Strange Gods, and D. H. Lawrence’s Mexican fantasies suggest the anxiety of re-presentation that gripped the culture.

[8] Davis and Hersh (21) divide probability theory into three aspects: 1) theory, which has the same status as any other branch of mathematics; 2) applied theory that is connected to experimentation’s descriptive goals; and 3) applied probability for practical decisions and actions.

[9] For primary documents, see Jean Van Heijenoort, From Frege to Gödel: a Source Book in Mathematical Logic, 1879-1931 (1967). Ernest Nagel and James Newman, Gödel’s Proof (1958) explains the steps of Gödel’s proofs and carefully restricts their metaphoric meanings; Douglas Hofstadter, Gödel, Escher, Bach: An Eternal Golden Braid [A Metaphoric Fugue on Minds and Machines in the Spirit of Lewis Carroll] (1980) places the work in the conceptual history that now leads to the possibility of artificial intelligence.

[10] See Richard Nash, John Craige’s Mathematical Principles of Christian Theology. (1991) for a discussion of the 17th Century mathematician and theologian who attempted to calculate the rate of decline of faith in the Gospels so that he would know the date of the Apocalypse. His contributions to calculus and statistics emerge in a context we find absurd, even if his friend, Isaac Newton, found them valuable.

[11] An equally foundational problem – the mathematics of infinity – occupies a similar position to the questions addressed by Gödel. Cantor’s opening of set theory exposes and solves the problems it poses to formal mathematics.

[12] For the historical appearances of the masculine version of this anxiety, see Dennis Todd’s Imagining Monsters: Miscreations of the Self in Eighteenth Century England (1995).

_____

Works Cited

• Aczel, Amir. 2015. Finding Zero: A Mathematician’s Odyssey to Uncover the Origins of Numbers. New York: St. Martin’s Griffin.
• Alexander, Amir. 2014. Infinitesimal: How a Dangerous Mathematical Theory Shaped the Modern World. New York: Macmillan.
• Anderson, Chris. 2008. “The End of Theory.” Wired Magazine 16, no. 7: 16-07.
• Beckett, Samuel. 1957. Murphy (1938). New York: Grove.
• Berk, Richard. 2011. “Q&A with Richard Berk.” Interview by Greg Johnson. PennCurrent (Dec 15).
• Blanchette, Patricia. 2014. “The Frege-Hilbert Controversy.” In Edward N. Zalta, ed., The Stanford Encyclopedia of Philosophy.
• boyd, danah, and Crawford, Kate. 2012. “Critical Questions for Big Data.” Information, Communication & Society 15:5. doi 10.1080/1369118X.2012.678878.
• de Certeau, Michel. 1988. The Practice of Everyday Life. Translated by Steven Rendall. Berkeley: University of California Press.
• Davis, Philip and Reuben Hersh. 1981. Descartes’ Dream: The World According to Mathematics. Boston: Houghton Mifflin.
• Desrosières, Alain, and Camille Naish. 2002. The Politics of Large Numbers: A History of Statistical Reasoning. Cambridge: Harvard University Press.
• Eagle, Christopher. 2007. “‘Thou Serpent That Name Best’: On Adamic Language and Obscurity in Paradise Lost.” Milton Quarterly 41:3. 183-194.
• Fenichel, Otto. 1945. The Psychoanalytic Theory of Neurosis. New York: W. W. Norton & Company.
• Gibson, Andrew. 2006. Beckett and Badiou: The Pathos of Intermittency. New York: Oxford University Press.
• Goldstein, Rebecca. 2006. Incompleteness: The Proof and Paradox of Kurt Gödel. New York: W.W. Norton & Company.
• Guthrie, William Keith Chambers. 1962. A History of Greek Philosophy: Vol.1 The Earlier Presocratics and the Pythagoreans. Cambridge: Cambridge University Press.
• Hofstadter, Douglas. 1979. Gödel, Escher, Bach: An Eternal Golden Braid; [a Metaphoric Fugue on Minds and Machines in the Spirit of Lewis Carroll]. New York: Basic Books.
• Kermode, Frank. 2000. The Sense of an Ending: Studies in the Theory of Fiction with a New Epilogue. New York: Oxford University Press.
• Kline, Morris. 1990. Mathematics: The Loss of Certainty. New York: Oxford University Press.
• Latour, Bruno. 1993. We Have Never Been Modern. Translated by Catherine Porter. Cambridge: Harvard University Press.
• Mitchell, W. J. T. 1995. Picture Theory: Essays on Verbal and Visual Representation. Chicago: University of Chicago Press.
• Nagel, Ernest and James Newman. 1958. Gödel’s Proof. New York: New York University Press.
• Office of Educational Technology at the US Department of Education. “Jose Ferreria: Knewton – Education Datapalooza”. Filmed [November 2012]. YouTube video, 9:47. Posted [November 2012]. https://youtube.com/watch?v=Lr7Z7ysDluQ.
• O’Neil, Cathy. 2016. Weapons of Math Destruction. New York: Crown.
• Pasquale, Frank. 2016. The Black Box Society: The Secret Algorithms that Control Money and Information. Cambridge: Harvard University Press.
• Pigliucci, Massimo. 2009. “The End of Theory in Science?”. EMBO Reports 10, no. 6.
• Porter, Theodore. 1986. The Rise of Statistical Thinking, 1820-1900. Princeton: Princeton University Press.
• Rotman, Brian. 1987. Signifying Nothing: The Semiotics of Zero. Stanford: Stanford University Press
• Rotman, Brian. 2000. Mathematics as Sign: Writing, Imagining, Counting. Stanford: Stanford University Press.
• Tegmark, Max. 2008. “The Mathematical Universe.” Foundations of Physics 38 no. 2: 101-150.
• Todd, Dennis. 1995. Imagining Monsters: Miscreations of the Self in Eighteenth Century England. Chicago: University of Chicago Press.
• Turchin, Valentin. 1977. The Phenomenon of Science. New York: Columbia University Press.
• Van Heijenoort, Jean. 1967. From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931. Vol. 9. Cambridge: Harvard University Press.
• Wigner, Eugene P. 1959. “The Unreasonable Effectiveness of Mathematics in the Natural Sciences.” Richard Courant Lecture in Mathematical Sciences delivered at New York University, May 11. Reprinted in Communications on Pure and Applied Mathematics 13:1 (1960). 1-14.
• Wu, Xiaolin, and Xi Zhang. 2016. “Automated Inference on Criminality using Face Images.” arXiv preprint: 1611.04135.